Fast Inv-Sqrt Algorithm In Quake III

Posted on | Edited on | In
This article tells you something about fast inv-sqrt algorithm implemented in Quake III Arena.

Introduction

This article introduces the fast inv-sqrt algorithm, which is firstly used in Quake III Arena.

And btw, this article is simply translated from the blog I wrote on CSDN: https://blog.csdn.net/noahzuo/article/details/51555161

The Source Code

So here is the source code: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
float Q_rsqrt( float number ) 
{ 
    long i; 
    float x2, y; 
    const float threehalfs = 1.5F ;
    x2 = number * 0.5F ; 
    y = number ; 
    i = * ( long * ) &y; // evil floating point bit level hacking 
    i = 0x5f3759df - ( i >> 1 ); // what the fuck? 
    y = * ( float * ) &i; 
    y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration 
//  y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
    return y ;
}

And this function takes a 32-bit floating-point number $x$, and output the reciprocal of the square root $\frac{1}{\sqrt{x}}$of this number.

32-bit Floating-Point Number

Since this algorithm was designed with the IEEE 754-1985 32-bit floating-point specification in mind, it is necessary for us to get to know the structure of a floating-point number.

Float_example

You can refer to Single-precision floating-point format for more information and I’ll skip the explanation since this is not the point of this article.

In short, for a positive floating-point number $x$, we have

which $e_x$ is the 8-bit exponent and $m_x$ is the fraction part.

Moreover, to convert a floating-point number to a integer, we have

which L is $2^{23}$ and B is $127$.

Algorithm

Newton’s Method

We can find successively better approximations to the roots of a real-valued function using Newton's method.

Suppose a single-variable function $ f $ defined for a real variable $ x $, if the function satisfied sufficient assumptions and the initial guess is close, then

is a better approximation of the root than $x_{0}$.

The process is repeated as

until a sufficiently precise value is reached.

img

The process iteration is like:

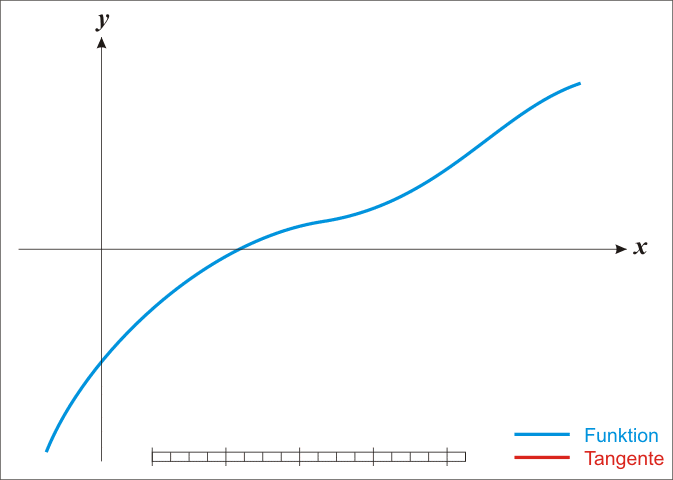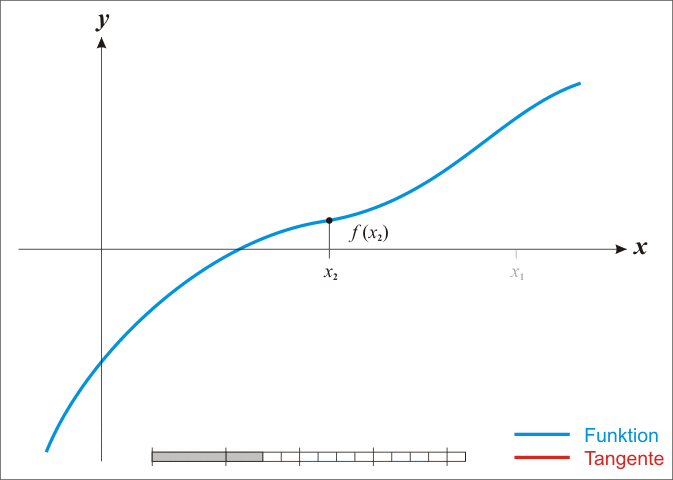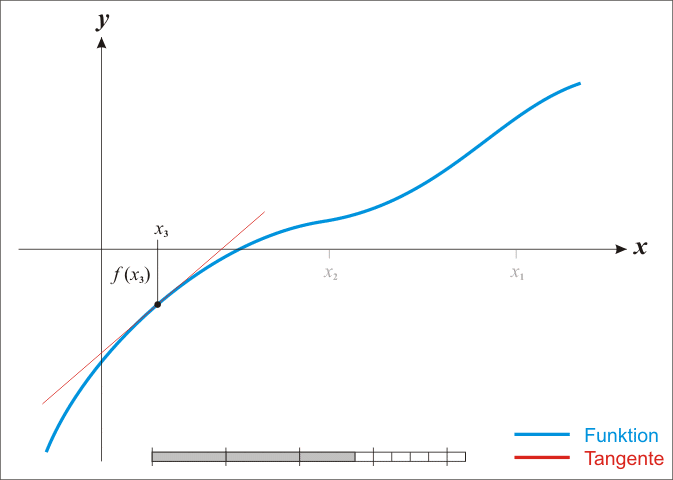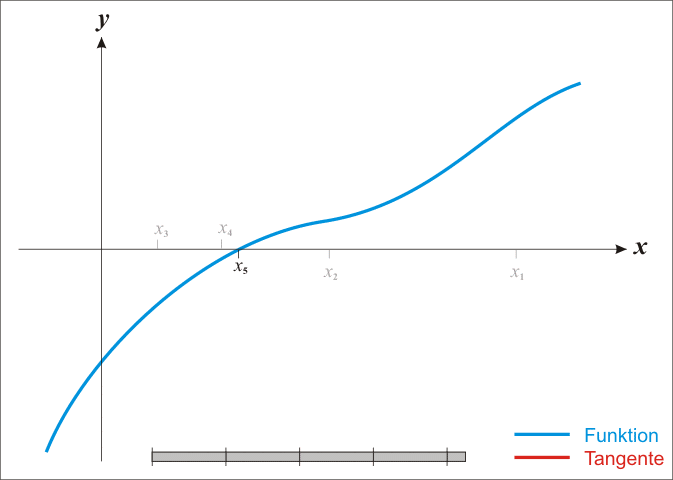
Illustration of Newton's method

Black Magic

The magic is i = 0x5f3759df - ( i >> 1 ), but how does it work?

For function

, firstly we have:

then we convert it to Newton's method style:

So for $ x = 2^{e{x}}(1 + m{x}) $, we have:

and since $m_{x} \in [0, 1)$, we have:

where $\sigma \approx 0.0430357$ yields the optimal approximation.

Thus there is the approximation

Finally we have:

I am so cute, please give me money...