GJK(Gilbert-Johnson-Keerthi) Algorithm for Collision Detection

What is GJK Algorithm?

GJK algorithm is proposed by Gilbert, Johnson and Keerthi for determining intersection between two polyhedra. It is one of the most effective methods.

As originally described, GJK is a simplex-based descent algorithm that, given two sets of vertices as iputs, finds the Euclidean distance(and closest points) between the convex hulls of these sets.

But actually the GJK algorithm can also be applied to arbitrary convex point sets, not just polyhedra.

An important point is that the GJK algorithm does not actually operate on the two input objects per se, but on the Minkowski difference between the objects. In short, GJK algorithm searches the Minkowski difference object iteratively, a subvolume at a time, each such volume being a simplex.

Minkowski Difference and Sum

For Point Sets

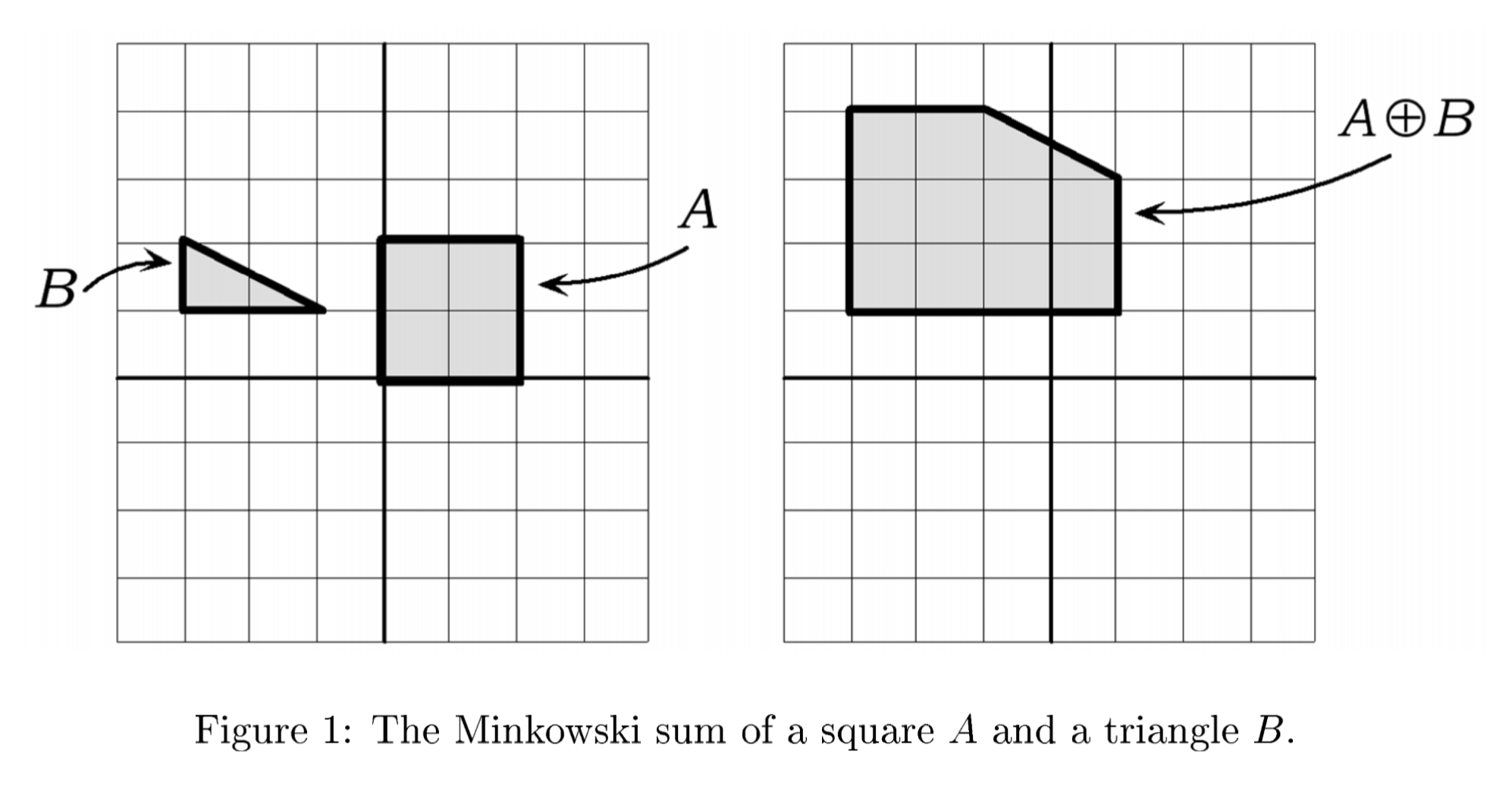
It is quite important to understand Minkowski sum and Minkowski difference of point sets for eventually understanding GJK algorithm. Let A and B be two point sets and let a and b be the position vectors corresponding to pairs of points in A and B. So the Minkowski sum, $A \oplus B$ is then defined as the set:

$$\begin{equation} \begin{aligned} A \oplus B = \lbrace a + b : a \in A, b \in B \rbrace \end{aligned} \end{equation}$$

In this equation, $a + b$ is the vector sum of the position vectors a and b. Visually the Minkowski sum can be seen as the region swept by A translated to every point in B(or vice versa). An illustration of the Minkowski sum is like this:

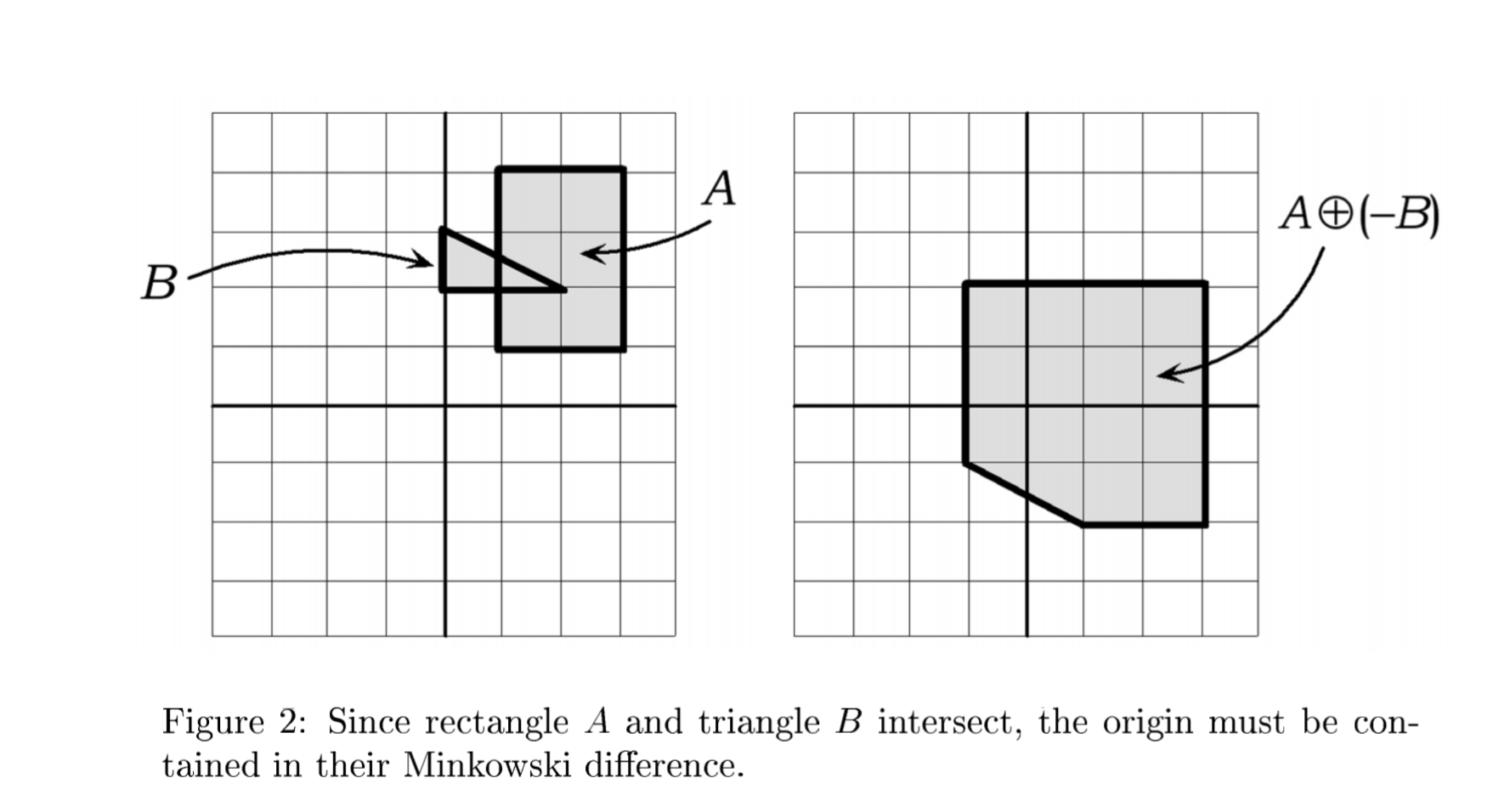
As for the Minkowski difference, it is defined analogously to the Minkowski sum:

$$\begin{equation} \begin{aligned} A \ominus B = \lbrace a - b : a \in A, b \in B \rbrace \end{aligned} \end{equation}$$

To make it more understandable, the Minkowski difference is obtained by adding A to the reflection of B about the origin. $A \ominus B = A \oplus ( - B)$：

For Convex Polyhedra

The Minkowski sum of two convex polyhedra $R = P \oplus Q$ has the property that R is a convex polygon and the vertices of R are sums of vertices of P and Q.

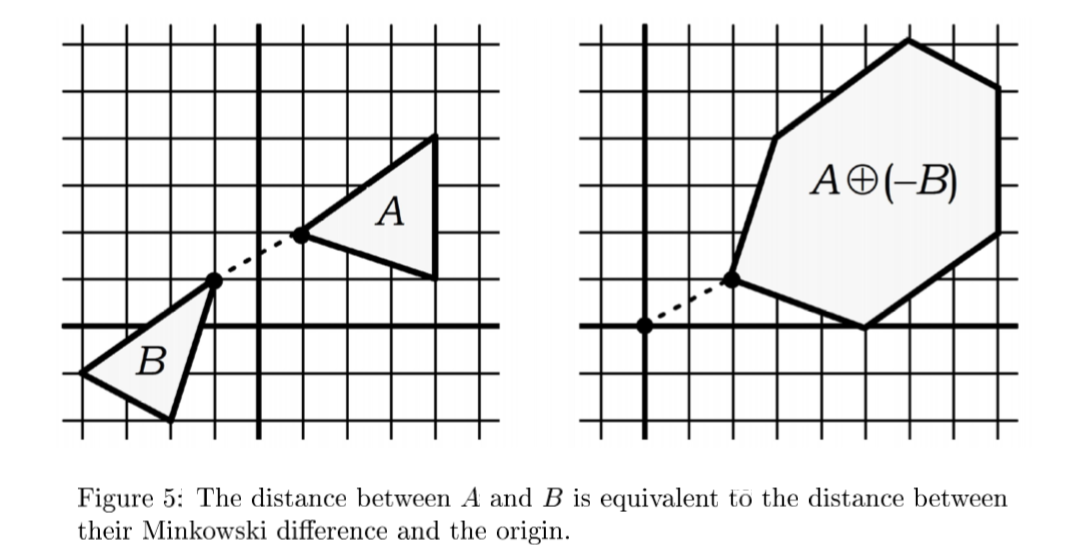
Minkowski difference is important for collision detection. If they intersect with each other, the origin must be contained in their Minkowski difference.

And in fact, it is possible to establish an even stronger result: computing the minimum distance between A and B is equivalent to computing the minimum distance between C and the origin:

$$\begin{equation} \begin{aligned} distance(A, B) & = min \lbrace \left\\| a - b \right\\| : a \in A, b \in B \rbrace \\\\ \ & = min \lbrace \left\\| c \right\\| : c \in A \ominus B \rbrace \end{aligned} \end{equation}$$

Supporting Point of a Simplex

Support point is very important for GJK-based collision detection. But what is the support point of a simplex?

For a given direction $d$ and a general convex set $C$, the point $P$ that has the most distant along $d$ is called a supporting point of $C$. More specifically, $P$ is a supporting point of $C$ if $d \dot P = max \lbrace d \dot V : V \in C \rbrace$, that is $P$ is a point for which $d \dot P$ is maximal like this:

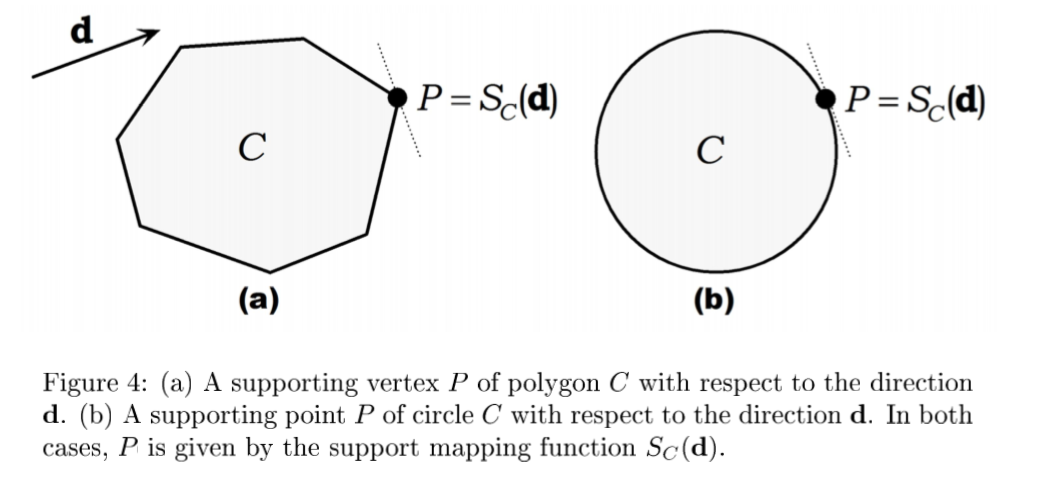
And we also need to know something called Support mapping. It is a function, $S_C(d)$, that maps the direction $d$ into a supporting point of $C$ of the convex set $C$.

We can have such mappings in a closed form for some simple shapes like boxes, spheres, cylinders and etc. For example, for a sphere $C$ centered at $O$ and with a radius of $r$, the support mapping is given by $S_C(d) = O + r \frac{d}{ \| d \d } $. And btw, this can lead to the separate axis theorem.

But for a polytope of n vertices, a supporting vertex is trivially found in $O(n)$ times by searching over all vertices. For performance optimization, we can find the extreme vertex through a simple hill-climbing algorithm. Since we only care about a simplex, we could gain so many performance using this method.

Core Algorithm

Just as we mentioned, the GJK algorithm effectively determines intersection between polyhedra by computing the Euclidean distance between them. To be more specific, The separation distance between two polyhedra $A$ and $B$ is equivalent to the shortest distance between their Minkowski difference $C$, $C = A \ominus B$, and the origin.

So, what we need to do is to find the point on C closest to origin. If we only want collision detection, we just need to determine whether the origin is located in the convex hull of $C$.

It seems we don’t gain so much performance using this method. However, a key point of the GJK algorithm is that it does not explicitly compute the Minkowski difference C. It only samples the Minkowski difference point set using a support mapping of $C = A \ominus B$. In short, we can use $s{A \ominus B} (d) = s{A}(d) - s_{B}(-d)$.

We still need to use Carathéodory’s theorem: For a convex body $H$ of $R^d$, each point of $H$ can be expressed as the convex combination of no more than $d + 1$ points from $H$. This means we only need to maintain a set up to $d + 1$ points.

So the core algorithm is:

1. Initialize the simplex set $Q$ to one or more points(up to $d + 1$ points, where $d$ is the dimension) from the Minkowski difference of $A$ and $B$.
2. Compute the point $P$ of minimum norm in the convex hull of $Q$(let’s call it $CH(Q)$).
3. If $P$ is already the origin, we can terminate the algorithm and return $A$ and $B$ as intersecting.
4. If the point $P$ is not the origin, we need to remove those points from $Q$ that does not determine the subsimplex of $Q$ in which $P$ lies.
5. And we need to move further to get the next point. Let $V = s{A \ominus B}(-P) = s{A}(-P) - s_{B}(P)$ be a supporting point in direction $-P$.
6. If there is not more distant point along the direction $-P$ than $P$, we simply stop and return $A$ and $B$ as not intersecting. And the separation distance is the length of the vector from the origin to $P$.
7. If there is such point $V$, add $V$ to $Q$ and go to stage 2.

Just check out the algorithm figure: